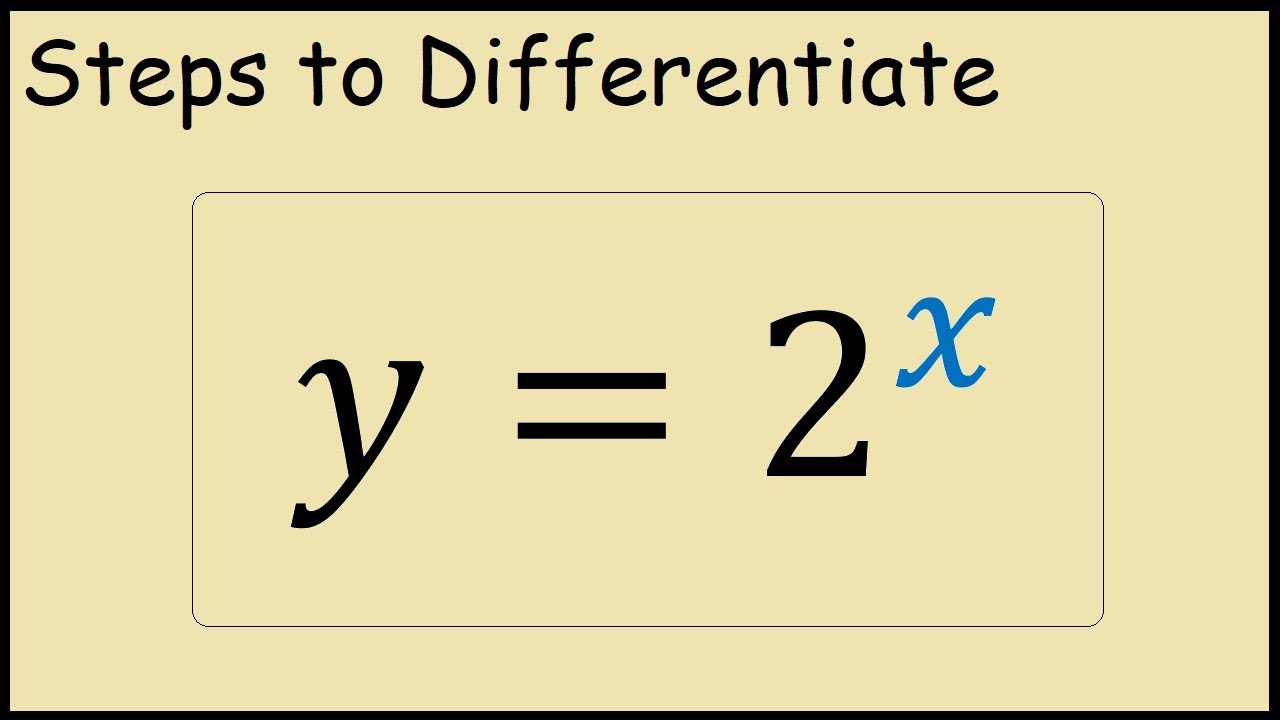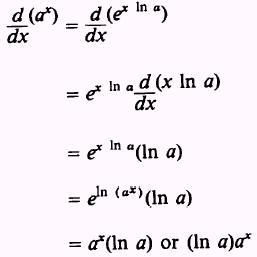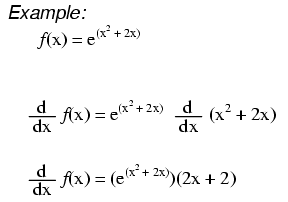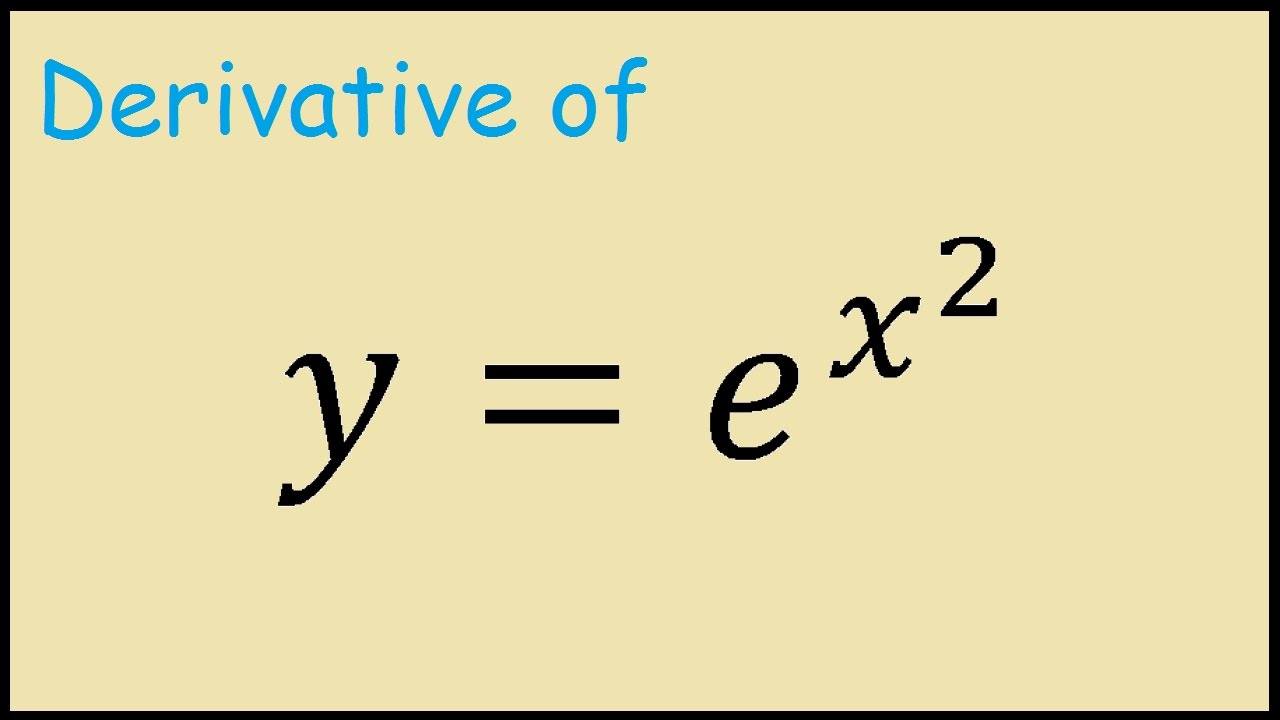A Power X Derivative

There are two ways we can find the derivative of x x.

A power x derivative. The derivative tells us the slope of a function at any point. Derivatives of functions with radicals square roots and other roots another useful property from algebra is the following. Dy dx y ln2 write y in terms of x dy dx 2 x. Find the derivative of the function.

Therefore derivative of 2 to the power of x is 2 x. Using this rule we can take a function written with a root and find its derivative using the power rule. I let y x x and take logarithms of both sides of this equation. There are rules we can follow to find many derivatives.

It s important to notice that this function is neither a power function of the form x k nor an exponential function of the form b x so we can t use the differentiation formulas for either of these cases directly. Here are useful rules to help you work out the derivatives of many functions with examples below. Learn how to find the derivative of any number raised to the power of x. We consider the series expression for the exponential function.

We need to find another method to find the first derivative of the above function. If y x x and x 0 then ln y ln x x use properties of logarithmic functions to expand the right side of. The derivative of e x. Note that the function defined by y x x is neither a power function of the form x k nor an exponential function of the form b x and the formulas of differentiation of these functions cannot be used.

An infinite polynomial is called a power series. Y 4 sqrt x 6 sqrt 3 x 2 solution. Example 3 find the derivative of the function y large frac 1 x normalsize large frac 2 x 2 normalsize large frac 3 x 3 normalsize. Ln2 this can be generalised as the derivative of a to the power of x where a is a constant a 0 is a x lna.

Let s do that with the exponential function. The neat thing about a power series is that to calculate its derivative you proceed just like you would with a polynomial.