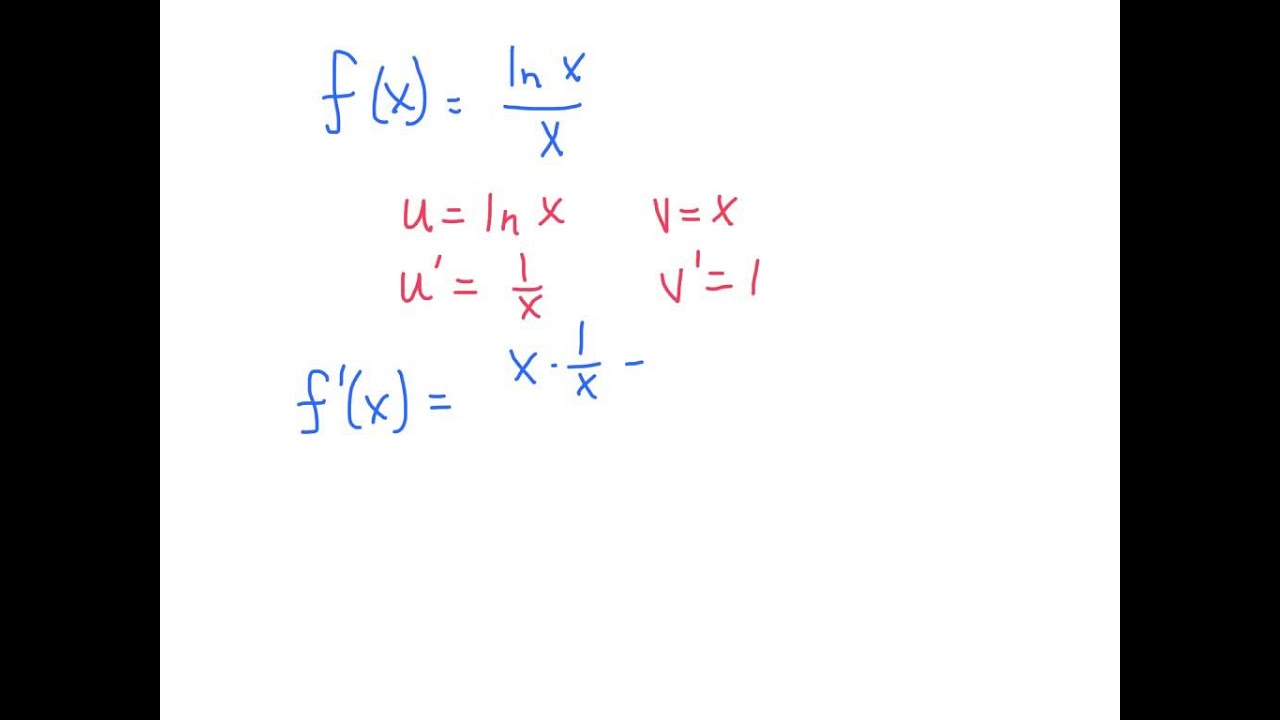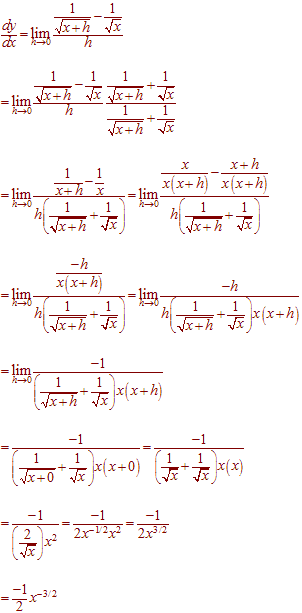A X Derivat

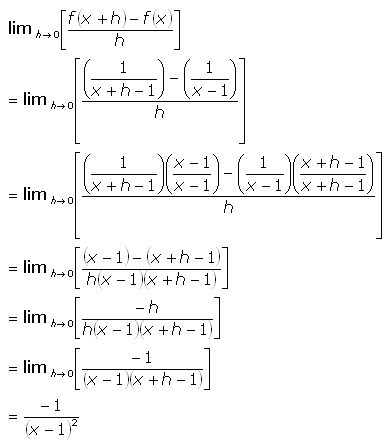
There are rules we can follow to find many derivatives.

A x derivat. Derivative examples example 1. The derivative calculator supports solving first second fourth derivatives as well as implicit differentiation and finding the zeros roots. X d dx ln y d dx x ln a 1 y dy dx x 0 ln a 1 ln a dy dx y ln a a x ln a. Then the second derivative at point x 0 f x 0 can indicate the type of that point.

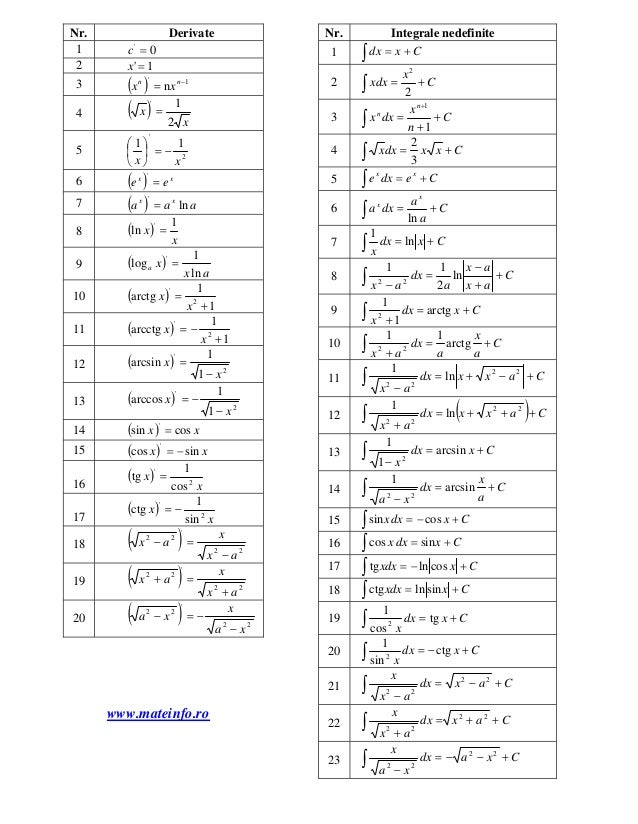
în cele ce urmează f și g sunt funcții de x iar c este o constantă. Derivatives of f x a x let s apply the definition of differentiation and see what happens. The derivative of the logarithmic function is given by. When the logarithmic function is given by.

The derivative calculator supports computing first second fifth derivatives as well as differentiating functions with many variables partial derivatives implicit differentiation and calculating roots zeros. The slope of a line like 2x is 2 or 3x is 3 etc. Let y a x taking logarithm on bothsideboth side ln y x ln a differentiating both side w r t. Găsirea derivatei este o operație primară în calculul diferențial acest tabel conține derivatele celor mai importante funcții precum și reguli de derivare pentru funcții compuse.

F x 1 x ln b x is the function argument. Funcțiile sunt presupuse reale de variabilă reală. The slope of a constant value like 3 is always 0. F x x 3 5x 2 x 8.

Here are useful rules to help you work out the derivatives of many functions with examples below. F x 3x 2 2 5x 1 0 3x 2 10x 1 example 2. Aceste formule sunt suficiente pentru a deriva orice funcție elementară. The derivative tells us the slope of a function at any point.

F x 0 0. You can also get a better visual and understanding of the function by using our graphing tool. Interactive graphs plots help visualize and better understand the functions. You can also check your answers.

F x cos 3x 2 3x 2 cos 3x 2 6x second derivative test. F x sin 3x 2. Free derivative calculator differentiate functions with all the steps. F x log b x.

Since the limit of as is less than 1 for and greater than for as one can show via direct calculations and since is a continuous function of for it follows that there exists a positive real number we ll call such that for we get. When the first derivative of a function is zero at point x 0.