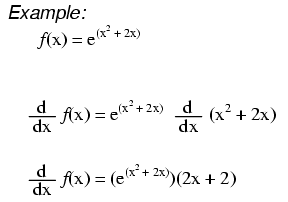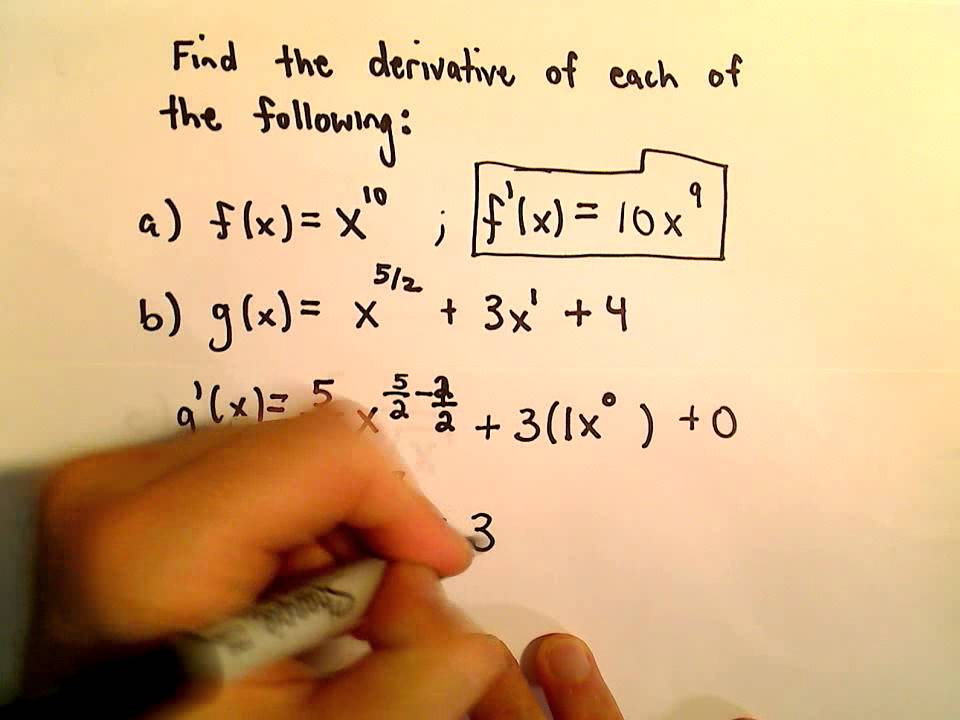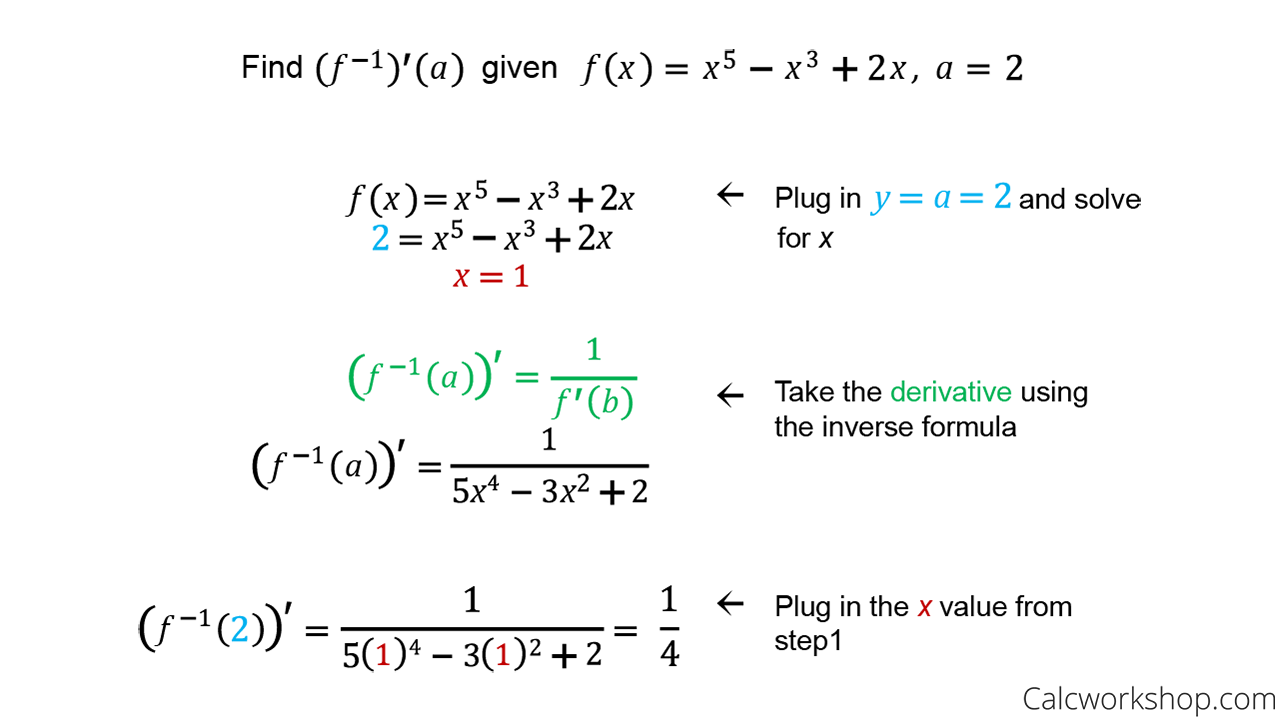A X Derivative Example

Changes in interest rates. Derivatives of f x a x let s apply the definition of differentiation and see what happens. Here are useful rules to help you work out the derivatives of many functions with examples below.

antena 3 dana grecu aniversare mesaje de la multi ani frumoase si scurte anp just ro posturi vacante annegret kramp karrenbauer kinder aniversare barbati felicitari de zi de nastere pentru barbati anotimpul toamna desene de toamna pentru scoala antecontract vanzare cumparare model annegret kramp karrenbauer mini rock

Maths First Institute Of Fundamental Sciences Massey University

Derivative Example

Calculus Exponential Derivatives Examples Solutions Videos

Definition Of Derivative Example Y 1 X Youtube

Learn How To Do Implicit Differentiation 7 Amazing Examples

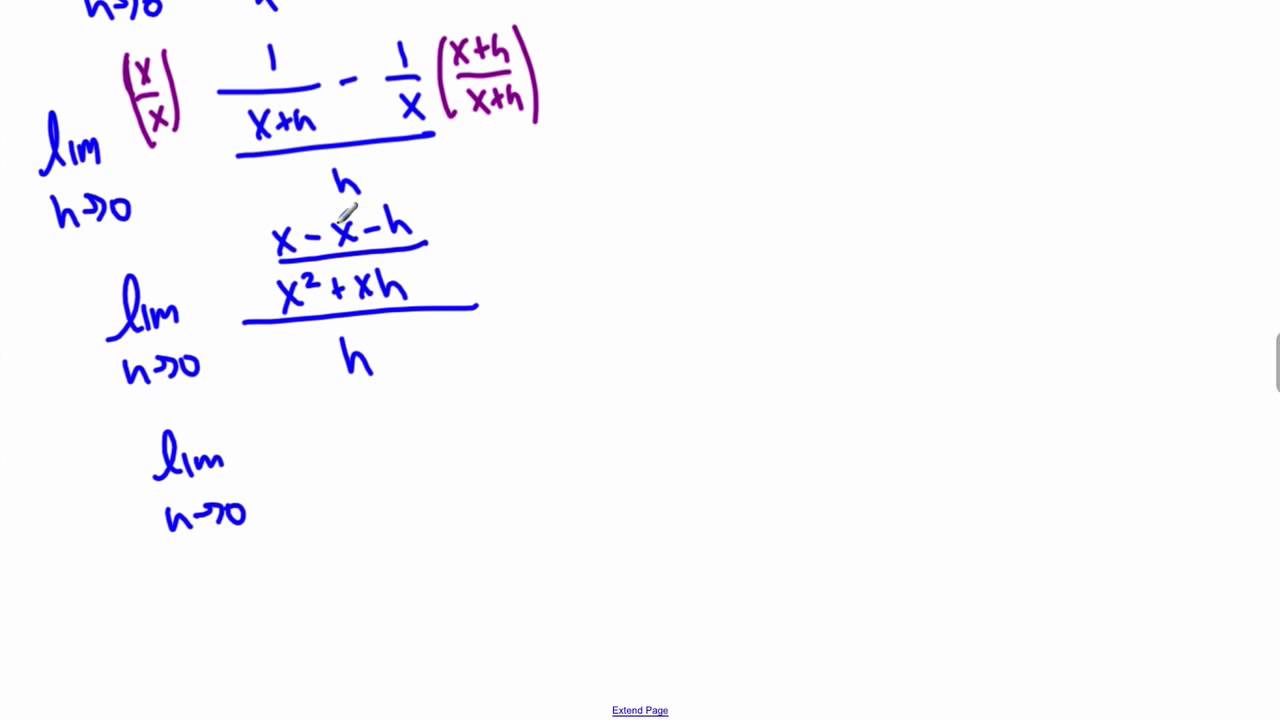
$Basic Derivative Rules And Derivative Formulas Such As The Chain Rule Power Rule$

Basic Derivative Rules And Derivative Formulas Such As The Chain Rule Power Rule

Let s look at an example.

A x derivative example. Let y x 2 1. There are rules we can follow to find many derivatives. Or we can find the slope in the y direction while keeping x fixed. The slope of a constant value like 3 is always 0.

The following diagram shows the derivatives of exponential functions. The slope of a line like 2x is 2 or 3x is 3 etc. Scroll down the page for more examples and solutions on how to use the derivatives of exponential functions. Find by definition the derivative of function x 2 1 with respect to x.

The second derivative is given by. Here is a function of one variable x. F x a x where a is a positive constant. One of the most commonly used derivatives is the option.

The derivative is the function slope or slope of the tangent line at point x. And weather events to name a few. F x x 2. When we find the slope in the x direction while keeping y fixed we have found a partial derivative.

Use the chain rule to calculate f as follows since u is the quotient of two function use the quotient rule to find u and substitute to obtain expand and group like terms. The derivative tells us the slope of a function at any point. A function for a surface that depends on two variables x and y. The derivative of a function is the ratio of the difference of function value f x at points x δx and x with δx when δx is infinitesimally small.

Derivative of the natural exponential function. Find the derivative of function f given by solution to example 11. Let y a x taking logarithm on bothsideboth side ln y x ln a differentiating both side w r t. In general an exponential function is of the form.

And its derivative using the power rule. Changes in foreign exchange rates. Fluctuations in stock bond commodity and index prices. Since the limit of as is less than 1 for and greater than for as one can show via direct calculations and since is a continuous function of for it follows that there exists a positive real number we ll call such that for we get.

X d dx ln y d dx x ln a 1 y dy dx x 0 ln a 1 ln a dy dx y ln a a x ln a. Function f is of the form u 1 4 with u x 6 x 5. Derivatives have been created to mitigate a remarkable number of risks.