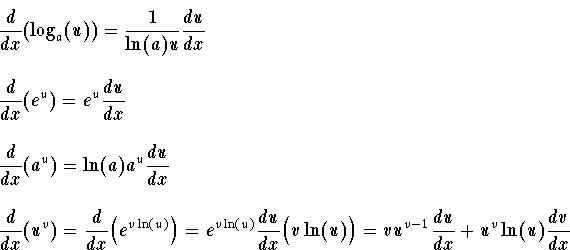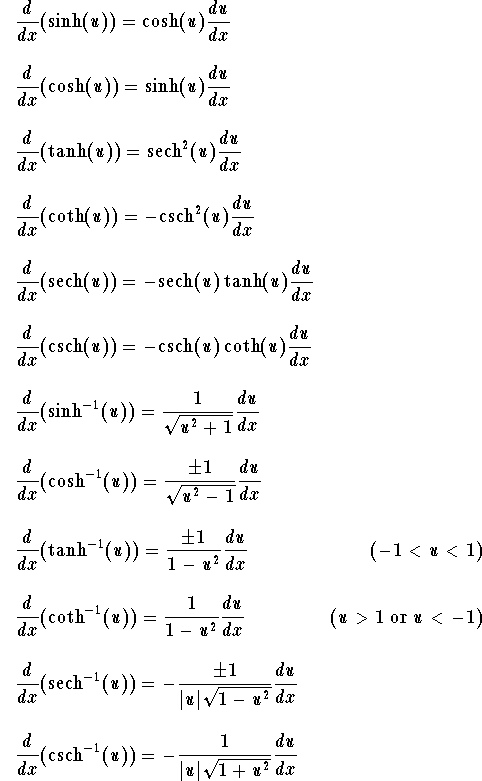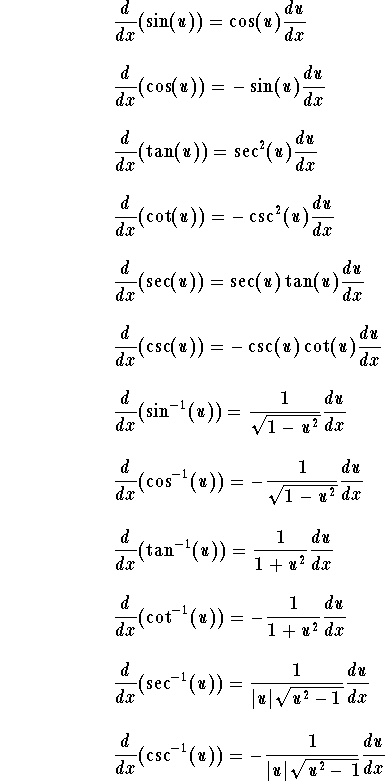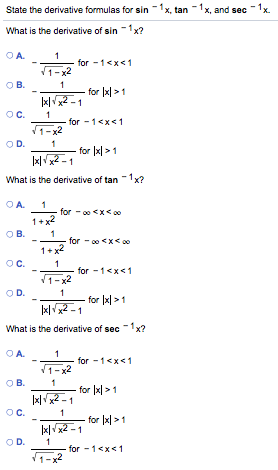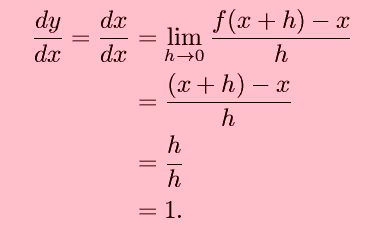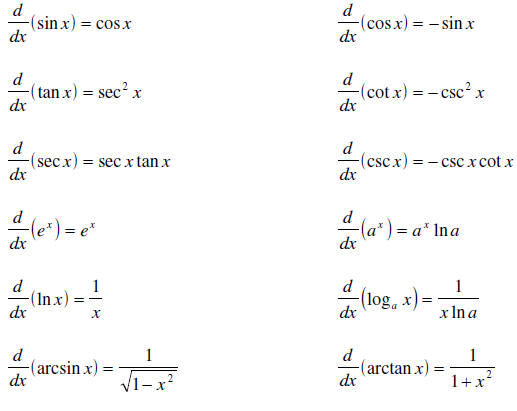A X Derivative Formula

The slope of a line like 2x is 2 or 3x is 3 etc.

A x derivative formula. The definition of the derivative. 3 frac d dx x 1 4 frac d dx f x n n f x n 1. Basic derivatives chain rule of derivatives derivative of the inverse function derivative of trigonometric functions etc. Just as before you take the log on both sides.

The slope of a constant value like 3 is always 0. Let y a x taking logarithm on bothsideboth side ln y x ln a differentiating both side w r t. Therefore the derivative function of f x is. Derivatives of f x a x let s apply the definition of differentiation and see what happens.

There are rules we can follow to find many derivatives. Since the limit of as is less than 1 for and greater than for as one can show via direct calculations and since is a continuous function of for it follows that there exists a positive real number we ll call such that for we get. Introduction to derivative of exponential function a x with respect to x formula with proof from first principle to prove d dx a x a x ln a. Hence if you did those earlier you should be able to do this one.

The derivative tells us the slope of a function at any point. Learn all the derivative formulas here. To find the derivative of y a x we use the exact same steps as that used for differentiating y e x and y x x as well. 2 frac d dx x n n x n 1 is called the power rule of derivatives.

Mathop lim limits x to a frac f left x right f left a right x a. Here are useful rules to help you work out the derivatives of many functions with examples below. This is one of the most important topics in higher class mathematics. Are given at byju s.

A differentiation formulas list has been provided here for students so that they can refer to these to solve problems based on differential equations. The general representation of the derivative is d dx. 1 f x 10x 4y what is the first derivative f x. X d dx ln y d dx x ln a 1 y dy dx x 0 ln a 1 ln a dy dx y ln a a x ln a.

In the first section of the limits chapter we saw that the computation of the slope of a tangent line the instantaneous rate of change of a function and the instantaneous velocity of an object at x a all required us to compute the following limit.